How Exactly Does Masking in Transformer Work
Posted on 2021-01-28Masking is one of those concepts that is easy to wave your hands at but quite important if you want to implement the Transformer from scratch.
Here I will only quickly recap how attention works in the context of transformer and then dive into code, but if you haven't grasped that, I highly recommend reading Jay Alammar's article The Illustrated Transformer first before continuing.
How Masking Works - A Recap
Masking just means we're telling the computer to pay zero attention to certain tokens. Therefore, it is not applied during the data processing stage but during the attention layer, where the attention weights are calculated.
Recall that attention layers essentially replace each token with a weighted average of the value vector of every token in the sentence, where the weight represents how much attention it pays to each of them. Formally:
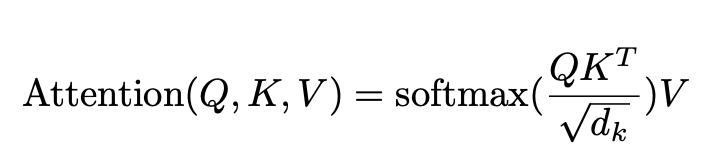
Let's say we're calculating the output for a token x1, we would take its query vector, multiply it with the key vector of every token in the sentence (including itself), scale that with a constant and then we'll get a score (the input to the softmax in the figure above), signifying how much attention x1 should pay to it. The higher the score a token gets, the more attention x1 should pay to that token. Then, to normalize the scores (or put them in relative terms), we pass them through a softmax. The closer the output of the softmax is to 1, the more attention x1 would pay to that token. Getting a softmax of 0 means x1 should pay zero attention to it.
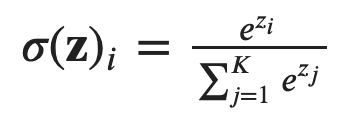
Here's the formula for softmax, where z represents the score. If z is -inf, the top of the fraction would be 0 and you will end up getting a 0 softmax (aka 0 attention).
This is why if we don't want a token to be seen, we set its score to -inf, because then its attention weight (softmax) would be 0. Notice again that the masking is applied to the SCORES in the attention layer, not the TOKENS in the input layer.
How Masking Works in Code
In terms of code, here's how to apply masking in PyTorch:
Let's picture your score tensor as a sheet of paper with grids.
The mask should have the exact shape of your score tensor (or at least broadcastable); picture it like another piece of sheet of paper.
You score tensor is a square matrix whose side is equal to the sentence length. It would look something like this:
| x1 | x2 | x3 | x4 | x5 | |
|---|---|---|---|---|---|
| x1 | 0.2 | 0.4 | 0.1 | 0.1 | 0.2 |
| x2 | 0.1 | 0.1 | 0.2 | 0.3 | 0.3 |
| x3 | 0 | 0.3 | 0.4 | 0.3 | 0 |
| x4 | 0.1 | 0 | 0 | 0.9 | 0 |
Where element (i, j) is how much attention score token i pays to token j. The mask should have the exact same shape.
In the most vanilla form, your mask should be filled with either True or False (where True's are in the grids/indices that you want to mask - intuitively, you tell the computer "true, yes, I want to mask that token").
You apply this mask to the score tensor in your attention layer by calling scores.masked_fill_(your_mask, float('-inf')). Visually, picture that you are laying your mask on top of the score tensor (literally, masking it). During the masked_fill_ method, wherever your mask tensor has a True value, imagine the computer just looks down at the exact same grid on the score tensor and set that value to float('-inf'), thus achieving the masking.
If you're using PyTorch's nn.Transformer out of the box, you just need to pass in the mask as one of the inputs to the model's forward function!
Feel free to email me (see icon below) if you have any questions or want to point out any mistakes that I may have made!
Appendix: Masking in PyTorch
If you're like me and are confused by all those masking functions PyTorch provides - here is a walkthrough.
If you look at the nn.Transformer's source code, you see that they provide a masking method out of the box.
def generate_square_subsequent_mask(self, sz: int) -> Tensor:
r"""Generate a square mask for the sequence. The masked positions are filled with float('-inf').
Unmasked positions are filled with float(0.0).
"""
mask = (torch.triu(torch.ones(sz, sz)) == 1).transpose(0, 1) # first type of mask
mask = mask.float().masked_fill(mask == 0, float('-inf')).masked_fill(mask == 1, float(0.0)) # second type of mask
return maskNotice that we can actually take the mask from the first assignment here and call it a day. It will give us the type of mask that I just mentioned. You apply it to your score tensor via masked_fill_. Let's call this the first type of mask.
But instead of a mask tensor filled with True or False, the actual return of this generate_square_subsequent_mask function is a mask tensor filled with 0 (where the first type of mask is True) and float(-inf) (where the first type of mask is False), you can apply it by adding it to the score tensor. Let's call this the second type of mask, or "additive mask" as the PyTorch docs calls it.
You can actually pass either type of masks into the forward function of nn.Transformer. Both are acceptable, because in the multi_head_attention_forward function in nn.functional , they check which type of mask you have passed in and apply it with the respective method (masked_fill_ or adding). Here is the exact piece of code:
if attn_mask is not None:
if attn_mask.dtype == torch.bool:
attn_output_weights.masked_fill_(attn_mask, float("-inf"))
else:
attn_output_weights += attn_mask