Recently, I have been reading a lot of machine learning papers and thought I would start sharing my notes to (1) back up my notes (2) share my digestion of these papers which might help other people understand. Please refer to the actual paper for details as I only sketch the main ideas here.

Title: Matching Networks for One-Shot Learning (2017), Vinyals et al.

Main Ideas: One-shot learning means learning to classify a class from a single labelled example (by using previous knowledge). In this paper, the transfer learning isn’t about using a pre-trained model but a previous dataset (called the support set).

Intuitively, we will train a neural network (f / g) to place the encodings of the same classes’ feature vectors close together geometrically, then when a new input feature vector comes, the neural network will place it geometrically closest to other feature vectors of the same class. The final prediction is a weighted average of all of x_i ‘s class (one-hot vectors, y_i), depending on their proximity to the input x. You will end up with a “softmax” and you take the largest class as the final prediction. (Another name for this model is “differentiable k-nearest neighbor”. K-nearest neighbor in the sense that you’re taking the weight average prediction of input x’s closest neighbor. Differentiable in the sense you’re training a f to output similar encoding for the x_i of same class)

This model is effective for one-shot learning because the network (f/g) becomes very good at identifying the relationship between classes rather than identifying any classes in particular. When given one single labelled image of a new class, the network knows to place it separately from the other classes. Then when it sees a second image of the same class in the test set, while it doesn’t know what class that image is itself, it knows that it is the same class as the one it saw previously. In other words, the network (f/g) can’t tell you which class it is, but CAN tell you which x_i in the support set it is most similar to, so you will then give the most weight to that x_i’s class (y_i).

Note that unlike a regular classification neural network, you need the original support set (x_i, y_i) available during the inference -- this is why Matching Network is sometimes called a neural network with external memory.

Formally, the model is:

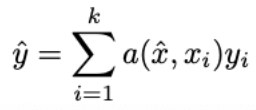
where

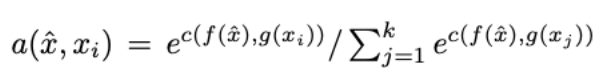
The training happens inside of a (attention) parameter, and what you’re really training are the two neural networks f and g (potentially f = g), which are similar to the Siamese Network which outputs similar encodings for inputs of the same class. Thus, a (attention) is really a weighting parameter that assigns greater weight to the class y_i depending on the similarity.

Full context encoding means that we encode x_i in the context of the entire support set S with a bidirectional LSTM with attention.

General Experiment Setup:

For training, you use a small mini-batch S(support set) of a few examples (e.g. up to 5) from a few classes (e.g. 5, so 25 examples in the mini-batch), get another min-batch B with the same label space (used for prediction based on S). You use S and the model to predict the examples in B, then look at their actual labels and update the gradients. The idea is that if the support set has seen a class before, the model should be able to correctly classify when it sees another example of the same class. (While this training method will yield a nonparametric model capable of predicting classes it hasn’t seen examples of before, it doesn’t work if the target label class distribution is too different i.e. the class you want to predict must be somewhat similar to the classes learned)

The paper describes three experiments: Omniglot, ImageNet (& mini ImageNet), Penn Treebank (language modeling). Omniglot has 1623 characters from 50 alphabets (classes). Use CNN as embedding function g.

Questions How do you iteratively select S and B exactly? Do you first make a hash map of {class1: [count, [[x₁, y₁] , [x₂, y₂], [x₃, y₃] ...] }? ← I can probably figure this out looking at the source code of implementations.

Other Notes Still need to delve further into the full context embedding method of f and g and how the two relate when f != g